How to Make a Hugs/Kisses Byzantine Jump Ring Chain

STEP 1: The Starter A

Close 2 jump rings, (pair A). Attach a small piece of wire to the end pair to create a handle. [For faster chain making, open jump rings and organize in piles of six rings.]

Size Selection: The following sizes can be used for Byzantine.

18ga 3.5mm ID (Small)
16ga 6.0mm ID (Large)

For Two Tone: Our example uses silver and gold. to create a two-tone chain, make pair A is always gold

STEP 2: The Starter B

Attach 2 new jump rings to pair A.

STEP 3: The Starter C

Attach 2 new jump rings to pair B.

STEP 4: The Grip

Hold the starter by the wire and let the jump rings hang. Use your thumb and finger so that you pinch Pair A & B. This isolation technique will make it easier to build your chain. If you move your hand, only pair C should move back and forth.

STEP 5: The Flip

Turn your hand so that you are pointing the starter at the ceiling. (C is now on top). Flip pair C open like the petals of a flower.

STEP 6: The Separation

Using an Awl or pointed tool, separate the rings of pair B. If you lose your place start over (step 4: the grip) and focus on pinching pair A/B to keep the rings from moving too much.

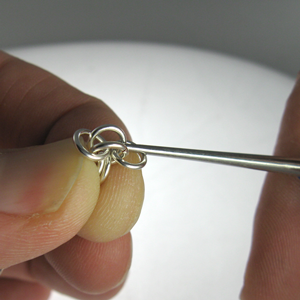STEP 7: The Push

Push the awl into the chain. The link should appear like the photo. You have used all 6 rings and the pattern now repeats.

Are your six rings open and ready?

STEP 8: The Push - Reviewed

Should look like this.

STEP 9: The Hold

Grasp the chain firmly. Prepare to remove the awl.

STEP 10: The Hold - Review

As you remove the Awl, maintain a firm pressure. This will keep the chain from collapsing while you pick up and add your next set of jump rings.

The Red shows the placement of the next ring

STEP 11: Insert New A

Insert a jump ring (new Pair A) onto the spot that was occupied by the awl. This may feel awkward at first, but you will quickly become proficient. I use a sweeping motion like setting a hook.

STEP 12: Insert New A - Review

Don’t put down the chain just yet. Reinsert the awl to hold your spot open. Whenever I need to put down my chain I always put the awl back in.

STEP 13: Close A and Add Another

Close the jump ring with a second plier. Work it back and forth with a slight inward pressure so there is no opening on the ring.

Don’t put down the chain just yet. Reinsert the awl to hold your spot open. Whenever I need to put down my chain I always put the awl back in.

Pick up another jump ring and place it next to the first

STEP 14: The New A

The pair of jump rings that you inserted in step 13 is now the new pair A (step 1)

STEP 15: The New B

Add two new jump rings to pair A.

STEP 16: The New C

Add two new rings to pair B.

Two-Tone:
A - Gold
B - Silver
C - Silver

STEP 17: Chain Review

REPEAT Steps 4 thru 13
The set of links divide the Florets, we call them nuts (made from 14 jump rings). You can make the nuts any length. Longer chain links work well for a necklace project.

STEP 18: Make a Floret

Begin by closing a 16ga 12mm ID jump ring (large).

Two-Tone:
All large rings would be gold (or other color)

STEP 19: Add a Ring

Attach one large ring to the first ring.

STEP 20: Organize

Organize the rings by pushing them together.

STEP 21: Link Three

Add a third ring thru the middle of the set of two.

STEP 22: Organize Again

Push all three rings together to make an organized 'floret'

STEP 23: Right Way, Wrong Way

If your floret looks slightly oval, the top ring may be laying incorrectly. Simply flip it over (while still attached) and it should nest correctly.

STEP 24: Attach Floret to Chain

In the beginning you will open up existing small rings to attach the floret. As you grow more confident, add the floret at step 16 when you create the flip and add pair A

STEP 25: New Pair A

Attach two new small rings to the floret and repeat the process starting at step 2

STEP 20: Add a Clasp

After the last flip, use a single jump ring to attach the clasp of your choice.